Bentuk Soal Pilihan Ganda
Soal Nomor 1
Jika $M = \{\text{faktor dari 15}\}$ dan $N =\{\text{bilangan}~\text{cacah kurang dari 7}\}$, maka $M \cup N = ....$
A. $\{0,3,5\}$
B. $\{1,3,5\}$
C. $\{0,2,4,6,7\}$
D. $\{0,1,2,3,4,5,6,15\}$
Diketahui:
$\begin{aligned} M & = \{1, 3, 5, 15\} \\ N & = \{0, 1, 2, 3, 4, 5, 6\}. \end{aligned}$
Dengan demikian, gabungan dari $M$ dan $N$ dinyatakan oleh
$M \cup N = \{0, 1, 2, 3, 4, 5, 6, 15\}.$
(Jawaban D)
$\begin{aligned} M & = \{1, 3, 5, 15\} \\ N & = \{0, 1, 2, 3, 4, 5, 6\}. \end{aligned}$
Dengan demikian, gabungan dari $M$ dan $N$ dinyatakan oleh
$M \cup N = \{0, 1, 2, 3, 4, 5, 6, 15\}.$
(Jawaban D)
Jika $K = \{x~|~5 \leq x \leq 9, x~\text{bilangan}~\text{asli}\}$ dan $L = \{x~|~7 \leq x < 13, x~\text{bilangan}~\text{cacah}\},$ maka $K \cup L = \cdots \cdot$
A. $\{5, 6, 7, 8, 9, 10, 11, 12, 13\}$
B. $\{5, 6, 7, 8, 9, 10, 11, 12\}$
C. $\{6, 7, 8, 9, 10\}$
D. $\{7, 8, 9, 10\}$
Pembahasan
Diketahui:
$\begin{aligned} K & = \{5, 6, 7, 8, 9\} \\ L & = \{7, 8, 9, 10, 11, 12\}. \end{aligned}$
Dengan demikian, gabungan dari $K$ dan $L$ dinyatakan oleh
$K \cup L = \{5,6,7,8,9,10,11,12\}.$
(Jawaban B)
Diketahui:
$\begin{aligned} K & = \{5, 6, 7, 8, 9\} \\ L & = \{7, 8, 9, 10, 11, 12\}. \end{aligned}$
Dengan demikian, gabungan dari $K$ dan $L$ dinyatakan oleh
$K \cup L = \{5,6,7,8,9,10,11,12\}.$
(Jawaban B)
Diketahui :
$A = \{x~|~1 < x < 20,x~\text{bilangan}~\text{prima}\}$ dan,
$B = \{y~|~1 \leq y \leq 10, y~\text{bilangan}~\text{ganjil}\}.$ Hasil dari $A \cap B =$....
A. $\{3, 5, 7\}$
B. $\{3, 5, 7, 9\}$
C. $\{1, 3, 5, 7\}$
D. $\{1, 3, 5, 7, 9\}$
Pembahasan
Diketahui:
$\begin{aligned} A & = \{2, 3, 5, 7, 11, 13, 17, 19\} \\ B & = \{1, 3, 5, 7, 9\}. \end{aligned}$
Dengan demikian, irisan dari $A$ dan $B$ dinyatakan oleh $A \cap B = \{3, 5, 7\}.$
(Jawaban A)
Diketahui:
$\begin{aligned} A & = \{2, 3, 5, 7, 11, 13, 17, 19\} \\ B & = \{1, 3, 5, 7, 9\}. \end{aligned}$
Dengan demikian, irisan dari $A$ dan $B$ dinyatakan oleh $A \cap B = \{3, 5, 7\}.$
(Jawaban A)
Soal Nomor 4
Perhatikan diagram Venn berikut.
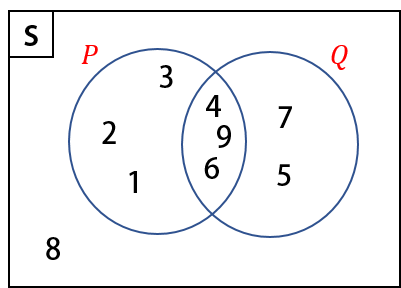
Himpunan yang anggota-anggotanya merupakan irisan $P$ dan $Q$ adalah $\cdots
\cdot$
A. $\{1, 2, 3, 4, 5, 6, 7, 8, 9\}$
B. $\{1, 2, 3, 4, 5, 6, 7, 9\}$
C. $\{1, 2, 3, 5, 7\}$
D. $\{4, 6, 9\}$
Soal Nomor 5
Dari diagram Venn di bawah, $P \cup Q = \cdots \cdot$

A. $\{2,3,5\}$
B. $\{1,4,6,7,8\}$
C. $\{1,2,3,4,5,6,7,8\}$
D. $\{1,2,3,4,5,6,7,8,9,10\}$
Soal Nomor 6
Perhatikan diagram Venn berikut.

Hasil dari $(P-Q) \cap R^C = \cdots \cdot$
A. $\{a, b\}$
B. $\{a, b, c\}$
C. $\{l, m, n\}$
D. $\{a, b, k, i\}$
Soal Nomor 7
Diketahui himpunan semesta $S$ adalah himpunan bilangan cacah yang kurang dari $20$. $A$ adalah himpunan bilangan prima antara $3$ dan $20$. $B$ adalah himpunan bilangan asli antara $2$ dan $15$. Komplemen dari $A \cup B$ adalah ....
A. $\{0,1,2,5,7,11,13,15,16,18\}$
B. $\{3,4,6,8,9,10,12,14,17,19\}$
C. $\{3,4,6,8,9,10,12,14,15,17,19\}$
D. $\{0,1,2,15,16,18\}$
Soal Nomor 8
A. $\{1, 2, 3, 4, 5, 6, 7, 8, 9\}$
B. $\{1, 2, 3, 4, 5, 6, 7, 9\}$
C. $\{1, 2, 3, 5, 7\}$
D. $\{4, 6, 9\}$
Pembahasan
Irisan $P$ dan $Q$ adalah bilangan yang menjadi anggota $P$ sekaligus anggota $Q$, yaitu $P \cap Q = \{4, 6, 9\}.$
(Jawaban D)
Irisan $P$ dan $Q$ adalah bilangan yang menjadi anggota $P$ sekaligus anggota $Q$, yaitu $P \cap Q = \{4, 6, 9\}.$
(Jawaban D)
Soal Nomor 5
Dari diagram Venn di bawah, $P \cup Q = \cdots \cdot$

A. $\{2,3,5\}$
B. $\{1,4,6,7,8\}$
C. $\{1,2,3,4,5,6,7,8\}$
D. $\{1,2,3,4,5,6,7,8,9,10\}$
Pembahasan
Notasi $P \cup Q$ (gabungan dari $P$ dan $Q$) artinya bilangan yang menjadi anggota $P$ atau $Q$, yaitu $P \cup Q = \{1, 2, 3, 4, 5, 6, 7, 8\}$. Tampak pada diagram Venn bahwa $\{9, 10\}$ berada di luar lingkaran, sehingga bukan anggota $P \cup Q$.
(Jawaban C)
Notasi $P \cup Q$ (gabungan dari $P$ dan $Q$) artinya bilangan yang menjadi anggota $P$ atau $Q$, yaitu $P \cup Q = \{1, 2, 3, 4, 5, 6, 7, 8\}$. Tampak pada diagram Venn bahwa $\{9, 10\}$ berada di luar lingkaran, sehingga bukan anggota $P \cup Q$.
(Jawaban C)
Soal Nomor 6
Perhatikan diagram Venn berikut.

Hasil dari $(P-Q) \cap R^C = \cdots \cdot$
A. $\{a, b\}$
B. $\{a, b, c\}$
C. $\{l, m, n\}$
D. $\{a, b, k, i\}$
Pembahasan
Berdasarkan diagram Venn di atas, diketahui
$\begin{aligned} P & = \{a, b, c, d, i, k\} \\ Q & = \{d, e, f, g, i, k\} \\ R & = \{c, d, g, h, j\}. \end{aligned}$
$P -Q$ atau dinotasikan juga sebagai $P \setminus Q$ (selisih $P$ dan $Q$) adalah anggota $P$ yang bukan anggota $Q$, yaitu $P -Q = \{a, b, c\}.$
$R^C$ (komplemen $R$) adalah anggota semesta yang bukan anggota $R$, yaitu
$R^C = \{a, b, e, f, i, k, m, l, n\}.$
Dengan demikian,
$\begin{aligned} & (P -Q) \cap R^C \\ & = \{a, b, c\} \cap \{a, b, e, f, i, k, m, l, n\} \\ & = \{a, b\}. \end{aligned}$
(Jawaban A)
Berdasarkan diagram Venn di atas, diketahui
$\begin{aligned} P & = \{a, b, c, d, i, k\} \\ Q & = \{d, e, f, g, i, k\} \\ R & = \{c, d, g, h, j\}. \end{aligned}$
$P -Q$ atau dinotasikan juga sebagai $P \setminus Q$ (selisih $P$ dan $Q$) adalah anggota $P$ yang bukan anggota $Q$, yaitu $P -Q = \{a, b, c\}.$
$R^C$ (komplemen $R$) adalah anggota semesta yang bukan anggota $R$, yaitu
$R^C = \{a, b, e, f, i, k, m, l, n\}.$
Dengan demikian,
$\begin{aligned} & (P -Q) \cap R^C \\ & = \{a, b, c\} \cap \{a, b, e, f, i, k, m, l, n\} \\ & = \{a, b\}. \end{aligned}$
(Jawaban A)
Soal Nomor 7
Diketahui himpunan semesta $S$ adalah himpunan bilangan cacah yang kurang dari $20$. $A$ adalah himpunan bilangan prima antara $3$ dan $20$. $B$ adalah himpunan bilangan asli antara $2$ dan $15$. Komplemen dari $A \cup B$ adalah ....
A. $\{0,1,2,5,7,11,13,15,16,18\}$
B. $\{3,4,6,8,9,10,12,14,17,19\}$
C. $\{3,4,6,8,9,10,12,14,15,17,19\}$
D. $\{0,1,2,15,16,18\}$
Pembahasan
Diketahui:
$\begin{aligned} S & = \{0, 1, 2, 3, \cdots, 18, 19\} \\ A & = \{5, 7, 11, 13, 17, 19\} \\ B & = \{3, 4, 5, \cdots, 13, 14\}. \end{aligned}$
Dengan demikian, gabungan dari $A$ dan $B$ dinyatakan oleh
$A \cup B = \{3, 4, 5, \cdots, 13, 14, 17, 19\}.$
Ini berarti, komplemen dari $A \cup B$ adalah
$(A \cup B)^C = \{0, 1, 2, 15, 16, 18\}.$
(Jawaban D)
Diketahui:
$\begin{aligned} S & = \{0, 1, 2, 3, \cdots, 18, 19\} \\ A & = \{5, 7, 11, 13, 17, 19\} \\ B & = \{3, 4, 5, \cdots, 13, 14\}. \end{aligned}$
Dengan demikian, gabungan dari $A$ dan $B$ dinyatakan oleh
$A \cup B = \{3, 4, 5, \cdots, 13, 14, 17, 19\}.$
Ini berarti, komplemen dari $A \cup B$ adalah
$(A \cup B)^C = \{0, 1, 2, 15, 16, 18\}.$
(Jawaban D)
Soal Nomor 8
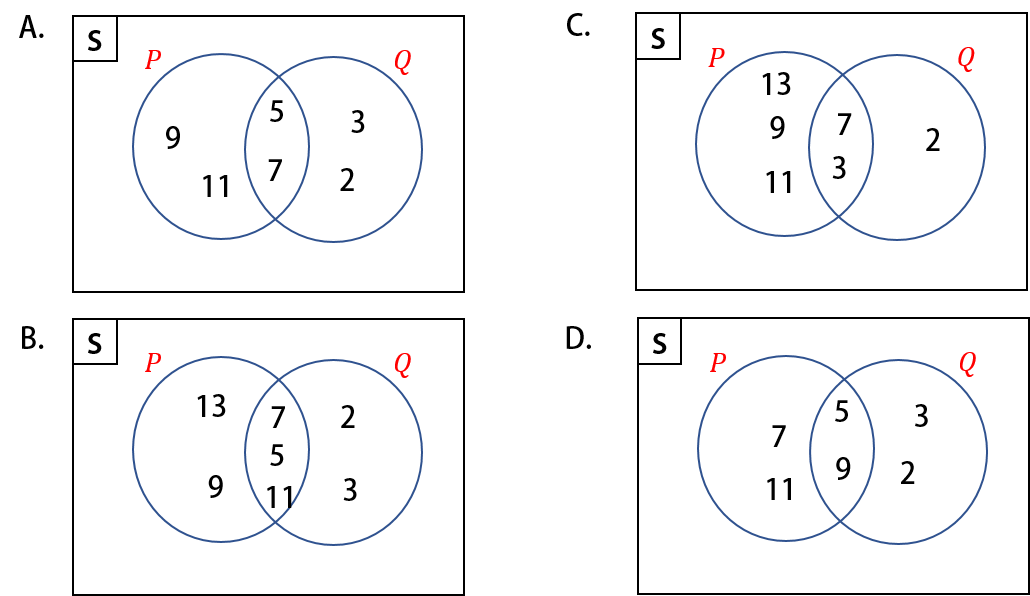
Diketahui $P = \{x~|~3 < x < 13,
x~\text{bilangan}~\text{ganjil}\}$ dan $Q = \{x~|~x < 11,
x~\text{bilangan}~\text{prima}\}$. Diagram Venn yang sesuai untuk kedua himpunan
tersebut adalah $\cdots \cdot$
Soal Nomor 9
Diketahui:
$$\begin{aligned} S & = \{x~|~x \leq 12, x~\text{bilangan}~\text{asli}\} \\ P & = \{x~|~1 \leq x < 12, x~\text{bilangan}~\text{prima}\} \\ Q & = \{x~|~1 \leq x \leq 12, x~\text{bilangan}~\text{ganjil}\} \end{aligned}$$Diagram Venn yang tepat untuk himpunan di atas adalah $\cdots \cdot$


Pembahasan
Dengan mendaftarkan anggota (tabulasi) masing-masing himpunan, diperoleh
$\begin{aligned} P & = \{5, 7, 9, 11\} \\ Q & = \{2, 3, 5, 7\}. \end{aligned}$
Irisan dari kedua himpunan ini adalah $P \cap Q = \{5, 7\}.$
Diagram Venn yang tepat untuk ini adalah pada pilihan A.
Dengan mendaftarkan anggota (tabulasi) masing-masing himpunan, diperoleh
$\begin{aligned} P & = \{5, 7, 9, 11\} \\ Q & = \{2, 3, 5, 7\}. \end{aligned}$
Irisan dari kedua himpunan ini adalah $P \cap Q = \{5, 7\}.$
Diagram Venn yang tepat untuk ini adalah pada pilihan A.
Soal Nomor 9
Diketahui:
$$\begin{aligned} S & = \{x~|~x \leq 12, x~\text{bilangan}~\text{asli}\} \\ P & = \{x~|~1 \leq x < 12, x~\text{bilangan}~\text{prima}\} \\ Q & = \{x~|~1 \leq x \leq 12, x~\text{bilangan}~\text{ganjil}\} \end{aligned}$$Diagram Venn yang tepat untuk himpunan di atas adalah $\cdots \cdot$

Pembahasan
Dengan mendaftarkan anggota (tabulasi) masing-masing himpunan, diperoleh
$\begin{aligned} S & = \{1, 2, 3, 4,5,6,7,8,9,10,11,12\} \\ P & = \{2, 3, 5, 7, 11\} \\ Q & = \{1, 3, 5, 7, 9, 11\}. \end{aligned}$
Irisan dari himpunan $P$ dan $Q$ adalah $P \cap Q =\{3, 5, 7, 11\},$
sedangkan komplemen dari gabungan $P$ dan $Q$ (anggota $S$ yang tidak menjadi anggota $P \cup Q$) adalah $(P \cup Q)^C = \{4, 6, 8, 10, 12\}.$
Ini berarti, bilangan $4,6,8,10,12$ berada di luar lingkaran pada diagram Venn.
Pilihan jawaban yang paling tepat adalah pilihan C.
Dengan mendaftarkan anggota (tabulasi) masing-masing himpunan, diperoleh
$\begin{aligned} S & = \{1, 2, 3, 4,5,6,7,8,9,10,11,12\} \\ P & = \{2, 3, 5, 7, 11\} \\ Q & = \{1, 3, 5, 7, 9, 11\}. \end{aligned}$
Irisan dari himpunan $P$ dan $Q$ adalah $P \cap Q =\{3, 5, 7, 11\},$
sedangkan komplemen dari gabungan $P$ dan $Q$ (anggota $S$ yang tidak menjadi anggota $P \cup Q$) adalah $(P \cup Q)^C = \{4, 6, 8, 10, 12\}.$
Ini berarti, bilangan $4,6,8,10,12$ berada di luar lingkaran pada diagram Venn.
Pilihan jawaban yang paling tepat adalah pilihan C.
Soal Nomor 10
Diketahui himpunan $$A = \{x~|~6 < x < 12, x \in \text{bilangan}~\text{cacah}\}.$$Banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota adalah $\cdots \cdot$
A. $5$ C. $15$
B. $10$ D. $32$
Pembahasan
Diketahui $A = \{7, 8, 9, 10, 11\}.$
Banyaknya anggota $A$ adalah $\text{n}(A) = 5.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$5$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$5$, diperoleh bahwa banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota adalah $\boxed{10}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota di mana banyak anggota $A$ seluruhnya ada $5$ adalah
$\begin{aligned} C^5_3 & = \dfrac{5!} {3! \cdot (5 -3)!} \\ & = \dfrac{5 \cdot 4 \cdot \cancel{3!} } {\cancel{3!} \cdot 2!} \\ & = \dfrac{5 \cdot 4}{2} = 10. \end{aligned}$
(Jawaban B)
Diketahui $A = \{7, 8, 9, 10, 11\}.$
Banyaknya anggota $A$ adalah $\text{n}(A) = 5.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$5$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$5$, diperoleh bahwa banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota adalah $\boxed{10}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota di mana banyak anggota $A$ seluruhnya ada $5$ adalah
$\begin{aligned} C^5_3 & = \dfrac{5!} {3! \cdot (5 -3)!} \\ & = \dfrac{5 \cdot 4 \cdot \cancel{3!} } {\cancel{3!} \cdot 2!} \\ & = \dfrac{5 \cdot 4}{2} = 10. \end{aligned}$
(Jawaban B)
Soal Nomor 11
Diketahui himpunan $K = \{1 < x \leq 11, x \in~\text{bilangan}~\text{ganjil}\}.$ Banyak himpunan bagian dari $K$ yang mempunyai $4$ anggota adalah $\cdots \cdot$
A. $5$ C. $20$
B. $10$ D. $35$
Pembahasan
Diketahui $K = \{3, 5, 7, 9, 11\}.$
Banyaknya anggota $K$ adalah $\text{n}(K) = 5.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$5$ seperti berikut.
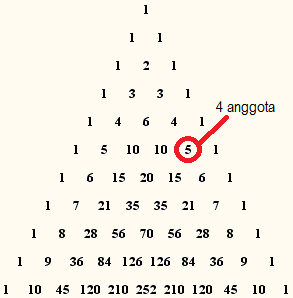
Berdasarkan bilangan yang ada pada tingkat ke-$5$, diperoleh bahwa banyak himpunan bagian dari $K$ yang mempunyai $4$ anggota adalah $\boxed{5}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $K$ yang mempunyai $4$ anggota di mana banyak anggota $K$ seluruhnya ada $5$ adalah
$\begin{aligned} C^5_4 & = \dfrac{5!} {4! \cdot (5 -4)!} \\ & = \dfrac{5 \cdot \cancel{4!} } {\cancel{4!} \cdot 1} = \dfrac{5}{1} = 5. \end{aligned}$
(Jawaban A)
Diketahui $K = \{3, 5, 7, 9, 11\}.$
Banyaknya anggota $K$ adalah $\text{n}(K) = 5.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$5$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$5$, diperoleh bahwa banyak himpunan bagian dari $K$ yang mempunyai $4$ anggota adalah $\boxed{5}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $K$ yang mempunyai $4$ anggota di mana banyak anggota $K$ seluruhnya ada $5$ adalah
$\begin{aligned} C^5_4 & = \dfrac{5!} {4! \cdot (5 -4)!} \\ & = \dfrac{5 \cdot \cancel{4!} } {\cancel{4!} \cdot 1} = \dfrac{5}{1} = 5. \end{aligned}$
(Jawaban A)
Soal Nomor 12
Diketahui himpunan $$B = \{x~|~2 < x \leq 17, x \in~\text{bilangan}~\text{prima}\}.$$Banyak himpunan bagian dari $B$ yang mempunyai $2$ anggota adalah $\cdots \cdot$
A. $6$ C. $15$
B. $10$ D. $21$
Pembahasan
Diketahui $B = \{3, 5, 7, 11, 13, 17\}.$
Banyaknya anggota $B$ adalah $\text{n}(B) = 6.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$6$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$6$, diperoleh bahwa banyak himpunan bagian dari $B$ yang mempunyai $2$ anggota adalah $\boxed{15}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $B$ yang mempunyai $2$ anggota di mana banyak anggota $B$ seluruhnya ada $6$ adalah
$\begin{aligned} C^6_2 & = \dfrac{6!} {2! \cdot (6 -2)!} \\ & = \dfrac{6 \cdot 5 \cdot \cancel{4!} } {2 \cdot \cancel{4!}} \\ & = \dfrac{6 \cdot 5}{2} = 15. \end{aligned}$
(Jawaban C)
Diketahui $B = \{3, 5, 7, 11, 13, 17\}.$
Banyaknya anggota $B$ adalah $\text{n}(B) = 6.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$6$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$6$, diperoleh bahwa banyak himpunan bagian dari $B$ yang mempunyai $2$ anggota adalah $\boxed{15}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $B$ yang mempunyai $2$ anggota di mana banyak anggota $B$ seluruhnya ada $6$ adalah
$\begin{aligned} C^6_2 & = \dfrac{6!} {2! \cdot (6 -2)!} \\ & = \dfrac{6 \cdot 5 \cdot \cancel{4!} } {2 \cdot \cancel{4!}} \\ & = \dfrac{6 \cdot 5}{2} = 15. \end{aligned}$
(Jawaban C)
Soal Nomor 13
Diketahui himpunan $P = \{x~|~x \leq 13, x \in~\text{bilangan}~\text{prima}\}$. Banyak himpunan bagian dari $P$ yang mempunyai $4$ anggota adalah $\cdots \cdot$
A. $25$ C. $12$
B. $15$ D. $7$
Pembahasan
Diketahui $P = \{2, 3, 5, 7, 11, 13\}.$
Banyaknya anggota $P$ adalah $\text{n}(P) = 6.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$6$ seperti berikut.
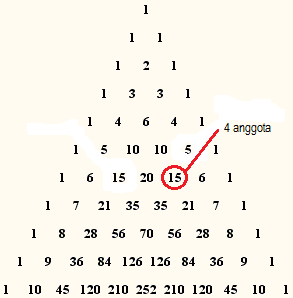
Berdasarkan bilangan yang ada pada tingkat ke-$6$, diperoleh bahwa banyak himpunan bagian dari $P$ yang mempunyai $4$ anggota adalah $\boxed{15}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $P$ yang mempunyai $4$ anggota di mana banyak anggota $P$ seluruhnya ada $6$ adalah
$\begin{aligned} C^6_4 & = \dfrac{6!} {4! \cdot (6 -4)!} \\ & = \dfrac{6 \cdot 5 \cdot \cancel{4!} } {\cancel{4!} \cdot 2!} \\ & = \dfrac{6 \cdot 5}{2} = 15. \end{aligned}$
(Jawaban B)
Diketahui $P = \{2, 3, 5, 7, 11, 13\}.$
Banyaknya anggota $P$ adalah $\text{n}(P) = 6.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$6$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$6$, diperoleh bahwa banyak himpunan bagian dari $P$ yang mempunyai $4$ anggota adalah $\boxed{15}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $P$ yang mempunyai $4$ anggota di mana banyak anggota $P$ seluruhnya ada $6$ adalah
$\begin{aligned} C^6_4 & = \dfrac{6!} {4! \cdot (6 -4)!} \\ & = \dfrac{6 \cdot 5 \cdot \cancel{4!} } {\cancel{4!} \cdot 2!} \\ & = \dfrac{6 \cdot 5}{2} = 15. \end{aligned}$
(Jawaban B)
Soal Nomor 14
Diketahui himpunan $A = \{x~|~x~\text{faktor dari 24}\}$. Banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota adalah $\cdots \cdot$
A. $24$ C. $56$
B. $36$ D. $72$
Pembahasan
Diketahui $A = \{1, 2, 3, 4, 6, 8, 12, 24\}.$
Banyaknya anggota $A$ adalah $\text{n}(A) = 8.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$8$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$8$, diperoleh bahwa banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota adalah $\boxed{56}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota di mana banyak anggota $A$ seluruhnya ada $8$ adalah
$\begin{aligned} C^8_3 & = \dfrac{8!} {3! \cdot (8 -3)!} \\ & = \dfrac{8 \cdot 7 \cdot 6 \cdot \cancel{5!} } {6 \cdot \cancel{5!}} \\ & = \dfrac{8 \cdot 7 \cdot 6}{6} = 56. \end{aligned}$
(Jawaban C)
[collapse]
Diketahui $A = \{1, 2, 3, 4, 6, 8, 12, 24\}.$
Banyaknya anggota $A$ adalah $\text{n}(A) = 8.$
Alternatif 1: Segitiga Pascal
Buat Segitiga Pascal sampai tingkat ke-$8$ seperti berikut.

Berdasarkan bilangan yang ada pada tingkat ke-$8$, diperoleh bahwa banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota adalah $\boxed{56}$
Alternatif 2: Aturan Kombinasi
Banyak himpunan bagian dari $A$ yang mempunyai $3$ anggota di mana banyak anggota $A$ seluruhnya ada $8$ adalah
$\begin{aligned} C^8_3 & = \dfrac{8!} {3! \cdot (8 -3)!} \\ & = \dfrac{8 \cdot 7 \cdot 6 \cdot \cancel{5!} } {6 \cdot \cancel{5!}} \\ & = \dfrac{8 \cdot 7 \cdot 6}{6} = 56. \end{aligned}$
(Jawaban C)
[collapse]
Misalkan $A = \{\text{bilangan}~\text{asli}\}$ dan $B = \{x~|~\sqrt{n} = x\}$. Di antara nilai-nilai $n$ berikut yang tidak memenuhi hubungan $B \subset A$ adalah $\cdots \cdot$
A. $1$ C. $9$
B. $3$ D. $16$
Pembahasan
$B \subset A$ (baca: $B$ himpunan bagian dari $A$) artinya semua anggota $B$ adalah anggota $A$. Dalam kasus ini, $B$ harus beranggotakan bilangan asli.
Diketahui $B = \{x~|~\sqrt{n} = x\}.$
Ketika kita memilih $n = 1$, maka $x = \sqrt{1} = 1$ (bilangan asli).
Ketika kita memilih $n = 3$, maka $x = \sqrt{3}$ (bukan bilangan asli).
Dari sini, kita tahu bahwa $n$ harus berupa bilangan kuadrat sempurna (lebih dari $0$).
Jadi, nilai $n$ yang tidak memenuhi hubungan tersebut adalah $n = 3$.
(Jawaban B)
$B \subset A$ (baca: $B$ himpunan bagian dari $A$) artinya semua anggota $B$ adalah anggota $A$. Dalam kasus ini, $B$ harus beranggotakan bilangan asli.
Diketahui $B = \{x~|~\sqrt{n} = x\}.$
Ketika kita memilih $n = 1$, maka $x = \sqrt{1} = 1$ (bilangan asli).
Ketika kita memilih $n = 3$, maka $x = \sqrt{3}$ (bukan bilangan asli).
Dari sini, kita tahu bahwa $n$ harus berupa bilangan kuadrat sempurna (lebih dari $0$).
Jadi, nilai $n$ yang tidak memenuhi hubungan tersebut adalah $n = 3$.
(Jawaban B)
Soal Nomor 16
Di antara sekelompok warga yang terdiri dari $50$ orang yang sedang berbelanja, $20$ orang membeli buah apel, $25$ orang membeli buah mangga, dan $5$ orang membeli kedua buah tersebut. Banyak warga yang tidak membeli keduanya adalah $\cdots \cdot$
A. $25$ orang C. $15$ orang
B. $20$ orang D. $10$ orang
Pembahasan
Perhatikan diagram Venn berikut.
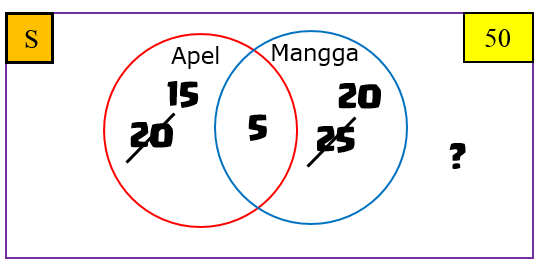
Banyak warga yang membeli buah apel atau buah mangga = $(20 -5) + (25 -5) + 5 = 40$ orang.
Banyak warga yang tidak membeli keduanya = $50 -40 = 10$ orang.
(Jawaban D)
Perhatikan diagram Venn berikut.

Banyak warga yang membeli buah apel atau buah mangga = $(20 -5) + (25 -5) + 5 = 40$ orang.
Banyak warga yang tidak membeli keduanya = $50 -40 = 10$ orang.
(Jawaban D)
Soal Nomor 17
Dari $50$ orang, terdapat $35$ orang berlangganan koran, $26$ orang berlangganan majalah, dan $7$ orang tidak berlangganan keduanya. Banyak orang yang hanya berlangganan tepat satu dari keduanya adalah $\cdots \cdot$
A. $8$ orang C. $18$ orang
B. $17$ orang D. $25$ orang
Pembahasan
Perhatikan diagram Venn berikut.

Banyak orang yang berlangganan koran atau majalah $= 50 -7 = 43$ orang.
Banyak orang yang berlangganan koran dan majalah $= 35 + 26 -43 = 18$ orang.
Banyak orang yang hanya berlangganan koran $= 35 -18 = 17$ orang.
Banyak orang yang hanya berlangganan majalah $= 26 -18 = 8$ orang.
Banyak orang yang berlangganan tepat satu dari keduanya $= 17 + 8 = 25$ orang.
(Jawaban D)
Perhatikan diagram Venn berikut.

Banyak orang yang berlangganan koran atau majalah $= 50 -7 = 43$ orang.
Banyak orang yang berlangganan koran dan majalah $= 35 + 26 -43 = 18$ orang.
Banyak orang yang hanya berlangganan koran $= 35 -18 = 17$ orang.
Banyak orang yang hanya berlangganan majalah $= 26 -18 = 8$ orang.
Banyak orang yang berlangganan tepat satu dari keduanya $= 17 + 8 = 25$ orang.
(Jawaban D)
Soal Nomor 18
Dari $100$ orang yang disurvei tentang kegemaran menonton acara televisi, diperoleh $68$ orang gemar menonton sinetron, $42$ orang gemar menonton berita, dan $10$ orang tidak gemar kedua acara tersebut. Banyak orang yang hanya gemar menonton berita adalah $\cdots \cdot$
A. $20$ orang C. $32$ orang
B. $22$ orang D. $36$ orang
Pembahasan
Perhatikan diagram Venn berikut.

Banyak orang yang gemar menonton sinetron atau berita $= 100 -10 = 90$ orang.
Banyak orang yang gemar menonton sinetron atau berita $= 68 + 42 -90 = 20$ orang.
(Dalam diagram Venn, nilai $x$ adalah $20$)
Banyak orang yang hanya gemar menonton berita $= 42 -20 = 22$ orang.
(Jawaban B)
Perhatikan diagram Venn berikut.

Banyak orang yang gemar menonton sinetron atau berita $= 100 -10 = 90$ orang.
Banyak orang yang gemar menonton sinetron atau berita $= 68 + 42 -90 = 20$ orang.
(Dalam diagram Venn, nilai $x$ adalah $20$)
Banyak orang yang hanya gemar menonton berita $= 42 -20 = 22$ orang.
(Jawaban B)
Soal Nomor 19
Dari $40$ orang anggota karang taruna, $21$ orang gemar bermain tenis meja, $27$ orang gemar bermain bulu tangkis, dan $15$ orang gemar keduanya. Banyak anggota karang taruna yang tidak gemar keduanya adalah ....
A. $6$ orang C. $12$ orang
B. $7$ orang D. $15$ orang
Pembahasan
Perhatikan diagram Venn berikut.
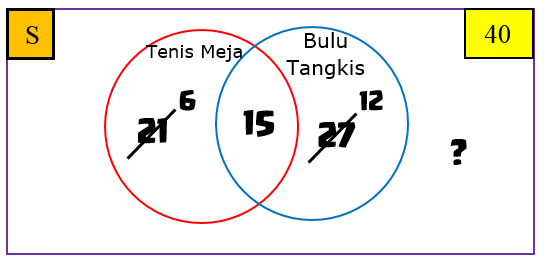
Banyak orang yang hanya gemar bermain tenis meja $= 21 -15 = 6$ orang.
Banyak orang yang hanya gemar bermain bulu tangkis $= 27 -15 = 12$ orang.
Banyak orang yang gemar bermain tenis meja atau bulu tangkis $= 6 + 12 + 15 = 33$ orang.
Banyak orang yang tidak gemar keduanya $= 40 -33 = 7$ orang.
(Jawaban B)
Perhatikan diagram Venn berikut.

Banyak orang yang hanya gemar bermain tenis meja $= 21 -15 = 6$ orang.
Banyak orang yang hanya gemar bermain bulu tangkis $= 27 -15 = 12$ orang.
Banyak orang yang gemar bermain tenis meja atau bulu tangkis $= 6 + 12 + 15 = 33$ orang.
Banyak orang yang tidak gemar keduanya $= 40 -33 = 7$ orang.
(Jawaban B)
Soal Nomor 20
Dalam suatu kelas yang terdiri dari $35$ anak, terdapat $25$ anak suka pelajaran matematika dan $20$ anak suka pelajaran fisika. Jika terdapat $3$ anak yang tidak suka pelajaran matematika maupun fisika, maka banyak anak yang suka kedua pelajaran itu adalah $\cdots \cdot$
A. $13$ orang C. $5$ orang
B. $7$ orang D. $3$ orang
Pembahasan
Perhatikan diagram Venn berikut.

Banyak orang yang suka pelajaran matematika atau fisika $= 35 -3 = 32$ orang.
Banyak orang yang suka pelajaran matematika sekaligus fisika $= 25 + 20 -32 = 13$ orang.
(Dalam diagram Venn, nilai $x$ adalah $13$)
(Jawaban A)
Perhatikan diagram Venn berikut.

Banyak orang yang suka pelajaran matematika atau fisika $= 35 -3 = 32$ orang.
Banyak orang yang suka pelajaran matematika sekaligus fisika $= 25 + 20 -32 = 13$ orang.
(Dalam diagram Venn, nilai $x$ adalah $13$)
(Jawaban A)
Soal Nomor 21
Dari $38$ siswa di kelas IX-A, $20$ siswa gemar matematika, $24$ siswa gemar olahraga, dan $6$ siswa tidak gemar matematika maupun olahraga. Banyak siswa yang hanya gemar matematika adalah $\cdots \cdot$
A. $4$ orang C. $8$ orang
B. $7$ orang D. $11$ orang
Pembahasan
Perhatikan diagram Venn berikut.

Banyak siswa yang gemar matematika atau olahraga $= 38 -6 = 32$ orang.
Banyak siswa yang gemar matematika dan olahraga $= 20 + 24 -32 = 12$ orang.
(Dalam diagram Venn, nilai $x$ adalah $12$)
Banyak siswa yang hanya gemar matematika $= 20 -12 = 8$ orang.
(Jawaban C)
Perhatikan diagram Venn berikut.

Banyak siswa yang gemar matematika atau olahraga $= 38 -6 = 32$ orang.
Banyak siswa yang gemar matematika dan olahraga $= 20 + 24 -32 = 12$ orang.
(Dalam diagram Venn, nilai $x$ adalah $12$)
Banyak siswa yang hanya gemar matematika $= 20 -12 = 8$ orang.
(Jawaban C)
Soal Nomor 22
Dari 49 siswa, diperoleh data sebagai berikut: $34$ siswa gemar bermain futsal, $28$ siswa gemar bermain basket, serta $6$ siswa tidak gemar bermain futsal maupun basket. Banyak siswa yang gemar keduanya adalah $\cdots \cdot$
A. $9$ orang C. $19$ orang
B. $17$ orang D. $21$ orang
Pembahasan
Perhatikan diagram Venn berikut.

Banyak siswa yang gemar bermain futsal atau basket $= 49 -6 = 43$ orang.
Banyak siswa yang gemar bermain futsal dan basket $= 34 + 28 -43 = 19$ orang.
(Dalam diagram Venn, nilai $x$ adalah $19$)
Jadi, banyak siswa yang gemar keduanya adalah $19$ orang.
(Jawaban C)
Perhatikan diagram Venn berikut.

Banyak siswa yang gemar bermain futsal atau basket $= 49 -6 = 43$ orang.
Banyak siswa yang gemar bermain futsal dan basket $= 34 + 28 -43 = 19$ orang.
(Dalam diagram Venn, nilai $x$ adalah $19$)
Jadi, banyak siswa yang gemar keduanya adalah $19$ orang.
(Jawaban C)
Soal Nomor 23
Wawancara dari $40$ orang pembaca majalah diketahui $5$ orang suka membaca majalah tentang politik dan olahraga, $9$ orang tidak menyukai keduanya. Banyak pembaca yang menyukai majalah olahraga sama dengan dua kali banyak pembaca yang menyukai majalah politik. Banyak pembaca yang menyukai majalah politik adalah $\cdots \cdot$
A. $8$ orang C. $12$ orang
B. $10$ orang D. $14$ orang
Pembahasan
Perhatikan diagram Venn berikut.
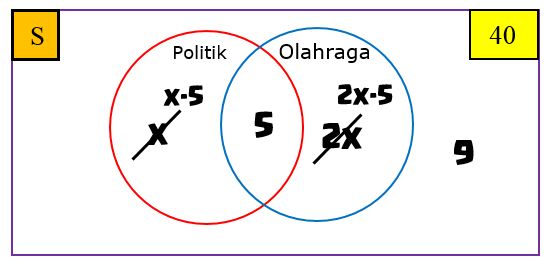
Misalkan banyak orang yang menyukai majalah politik adalah $x$, sedangkan banyak orang yang menyukai majalah olahraga adalah $2x.$
Banyak orang yang hanya menyukai majalah politik $= (x-5)$ orang.
Banyak orang yang hanya menyukai majalah olahraga $= (2x-5)$ orang.
Banyak orang yang menyukai majalah politik atau olahraga $= 40 -9 = 31$ orang.
Dengan demikian, dapat kita tulis
$\begin{aligned} (x-5) + 5 + (2x -5) & = 31 \\ 3x -5 & = 31 \\ 3x & = 36 \\ x & = 12. \end{aligned}$
Jadi, ada $12$ orang yang menyukai majalah politik.
(Jawaban C)
Perhatikan diagram Venn berikut.

Misalkan banyak orang yang menyukai majalah politik adalah $x$, sedangkan banyak orang yang menyukai majalah olahraga adalah $2x.$
Banyak orang yang hanya menyukai majalah politik $= (x-5)$ orang.
Banyak orang yang hanya menyukai majalah olahraga $= (2x-5)$ orang.
Banyak orang yang menyukai majalah politik atau olahraga $= 40 -9 = 31$ orang.
Dengan demikian, dapat kita tulis
$\begin{aligned} (x-5) + 5 + (2x -5) & = 31 \\ 3x -5 & = 31 \\ 3x & = 36 \\ x & = 12. \end{aligned}$
Jadi, ada $12$ orang yang menyukai majalah politik.
(Jawaban C)
Soal Nomor 24
Dalam sebuah kelompok yang terdiri dari $40$ orang, terdapat orang berambut hitam atau pirang dan mempunyai mata cokelat atau biru. Sebanyak $13$ orang berambut hitam dan bermata cokelat, $22$ orang berambut pirang, dan $19$ orang bermata biru. Banyaknya orang yang bermata cokelat dan berambut pirang adalah ....$
A. $5$ orang C. $14$ orang
B. $8$ orang D. $18$ orang
Pembahasan
Tabel berikut menyatakan jumlah orang berambut hitam, berambut pirang, bermata biru, dan bermata cokelat, seperti yang telah diketahui pada soal di atas.
$$\begin{array} {|c|c|c|c|} \hline & \text{Rambut Hitam} & \text{Rambut Pirang} & \text{Total} \\ \hline \text{Mata Cokelat} & 13 & & \\ \hline \text{Mata Biru} & & & 19 \\ \hline \text{Total} & & 22 & 40 \\ \hline \end{array}$$Total orang berambut hitam adalah $40-22=18,$ sedangkan total orang bermata cokelat adalah $40-19=21.$ Isi tabel akan tampak seperti berikut.
$$\begin{array} {|c|c|c|c|} \hline & \text{Rambut Hitam} & \text{Rambut Pirang} & \text{Total} \\ \hline \text{Mata Coklat} & 13 & & 21 \\ \hline \text{Mata Biru} & & & 19 \\ \hline \text{Total} & 18 & 22 & 40 \\ \hline \end{array}$$Banyak orang berambut pirang sama dengan $21-13=8.$ Banyak orang bermata biru sama dengan $18-13=5.$ Banyak orang berambut pirang sama dengan $19-5=14.$ Tabel akan lengkap seperti di bawah.
$$\begin{array} {|c|c|c|c|} \hline & \text{Rambut Hitam} & \text{Rambut Pirang} & \text{Total} \\ \hline \text{Mata Cokelat} & 13 & 8 & 21 \\ \hline \text{Mata Biru} & 5 & 14 & 19 \\ \hline \text{Total} & 18 & 22 & 40 \\ \hline \end{array}$$Berdasarkan tabel di atas, banyak orang yang berambut pirang dan bermata cokelat adalah $\boxed{8~\text{orang}}$
(Jawaban B)
Tabel berikut menyatakan jumlah orang berambut hitam, berambut pirang, bermata biru, dan bermata cokelat, seperti yang telah diketahui pada soal di atas.
$$\begin{array} {|c|c|c|c|} \hline & \text{Rambut Hitam} & \text{Rambut Pirang} & \text{Total} \\ \hline \text{Mata Cokelat} & 13 & & \\ \hline \text{Mata Biru} & & & 19 \\ \hline \text{Total} & & 22 & 40 \\ \hline \end{array}$$Total orang berambut hitam adalah $40-22=18,$ sedangkan total orang bermata cokelat adalah $40-19=21.$ Isi tabel akan tampak seperti berikut.
$$\begin{array} {|c|c|c|c|} \hline & \text{Rambut Hitam} & \text{Rambut Pirang} & \text{Total} \\ \hline \text{Mata Coklat} & 13 & & 21 \\ \hline \text{Mata Biru} & & & 19 \\ \hline \text{Total} & 18 & 22 & 40 \\ \hline \end{array}$$Banyak orang berambut pirang sama dengan $21-13=8.$ Banyak orang bermata biru sama dengan $18-13=5.$ Banyak orang berambut pirang sama dengan $19-5=14.$ Tabel akan lengkap seperti di bawah.
$$\begin{array} {|c|c|c|c|} \hline & \text{Rambut Hitam} & \text{Rambut Pirang} & \text{Total} \\ \hline \text{Mata Cokelat} & 13 & 8 & 21 \\ \hline \text{Mata Biru} & 5 & 14 & 19 \\ \hline \text{Total} & 18 & 22 & 40 \\ \hline \end{array}$$Berdasarkan tabel di atas, banyak orang yang berambut pirang dan bermata cokelat adalah $\boxed{8~\text{orang}}$
(Jawaban B)
Soal Nomor 25
Misalkan $\mathbb{N}$ menyatakan himpunan bilangan asli $\{1, 2, 3, \cdots\}.$ Jika $S = \{(-1)^n \mid n \in \mathbb{N}\},$ maka kardinalitas $S$ adalah $\cdots \cdot$
Catatan: Kardinalitas $S$ memiliki arti banyak anggota $S,$ umumnya dinotasikan $|S|.$
A. $0$ D. $3$
B. $1$ E. $\infty$
C. $2$
Pembahasan
Diketahui $S = \{(-1)^n \mid n \in \mathbb{N}\}.$
Jika kita menuliskan setiap anggota $S$ satu per satu dimulai dari $n = 1, 2, 3, \cdots,$ kita akan peroleh $S = \{-1, 1, -1, 1, \cdots\}$ yang memiliki arti bahwa
$$\begin{cases} 1 \in S~\text{jika}~n~\text{genap} \\ -1 \in S~\text{jika}~n~\text{ganjil}. \end{cases}$$Jadi, $S$ hanya memiliki dua anggota karena dapat ditulis $S = \{-1, 1\}$ sehingga kardinalitasnya adalah $\boxed{2}$
(Jawaban C)
Diketahui $S = \{(-1)^n \mid n \in \mathbb{N}\}.$
Jika kita menuliskan setiap anggota $S$ satu per satu dimulai dari $n = 1, 2, 3, \cdots,$ kita akan peroleh $S = \{-1, 1, -1, 1, \cdots\}$ yang memiliki arti bahwa
$$\begin{cases} 1 \in S~\text{jika}~n~\text{genap} \\ -1 \in S~\text{jika}~n~\text{ganjil}. \end{cases}$$Jadi, $S$ hanya memiliki dua anggota karena dapat ditulis $S = \{-1, 1\}$ sehingga kardinalitasnya adalah $\boxed{2}$
(Jawaban C)
Semoga postingan : Soal dan Pembahasan Materi Himpunan SMP ada manfaatnya. Salam Bahagia 👍















0 2:
Posting Komentar